„Frumusețea ecuațiilor simbolice este că este mult mai ușor să… vezi o problemă dintr-o privire”: Cum am trecut de la cuvinte și imagini la gândire simbolică

Pentru mulți, ideea de matematică va aduce înapoi ore nesfârșite de formule și ecuații la școală. Deci poate părea greu de imaginat, dar a fost o vreme când aritmetica nu exista. Desigur, mai era nevoie de a utiliza calcule complexe pentru a rezolva probleme din lumea reală, dar abia atunci când Muhammad ibn-Mūsā al-Khwārizmī, așa-numitul „părintele algebrei”, a stabilit bazele pentru rezolvarea ecuațiilor care am început să punem bazele modernului matematică.

În acest fragment din noua ei carte “Vector: O poveste surprinzătoare a spațiului, timpului și transformării matematice“, matematician Robyn Arianrhod explorează evoluția de 4.000 de ani a limbajului matematicii — de la descrieri complexe până la forma simbolică pe care o cunoaștem astăzi.

Învață să gândești simbolic

Algebra a făcut parte din matematică de când înregistrările au început acum aproape 4.000 de ani, dar nu întotdeauna în forma simbolică pe care o învățăm astăzi. De fapt, în cele mai multe dintre aceste patru milenii, a fost scris în întregime în cuvinte și cifre – deși lucrări precum celebrul manual al lui Euclid din 300 î.e.n.Elemente” a inclus și diagrame geometrice, pentru a ajuta la demonstrarea unor lucruri precum teorema lui Pitagorași pentru a arăta cum să extindem pătratele pe care le-am scrie astăzi ca (a+b)^2.

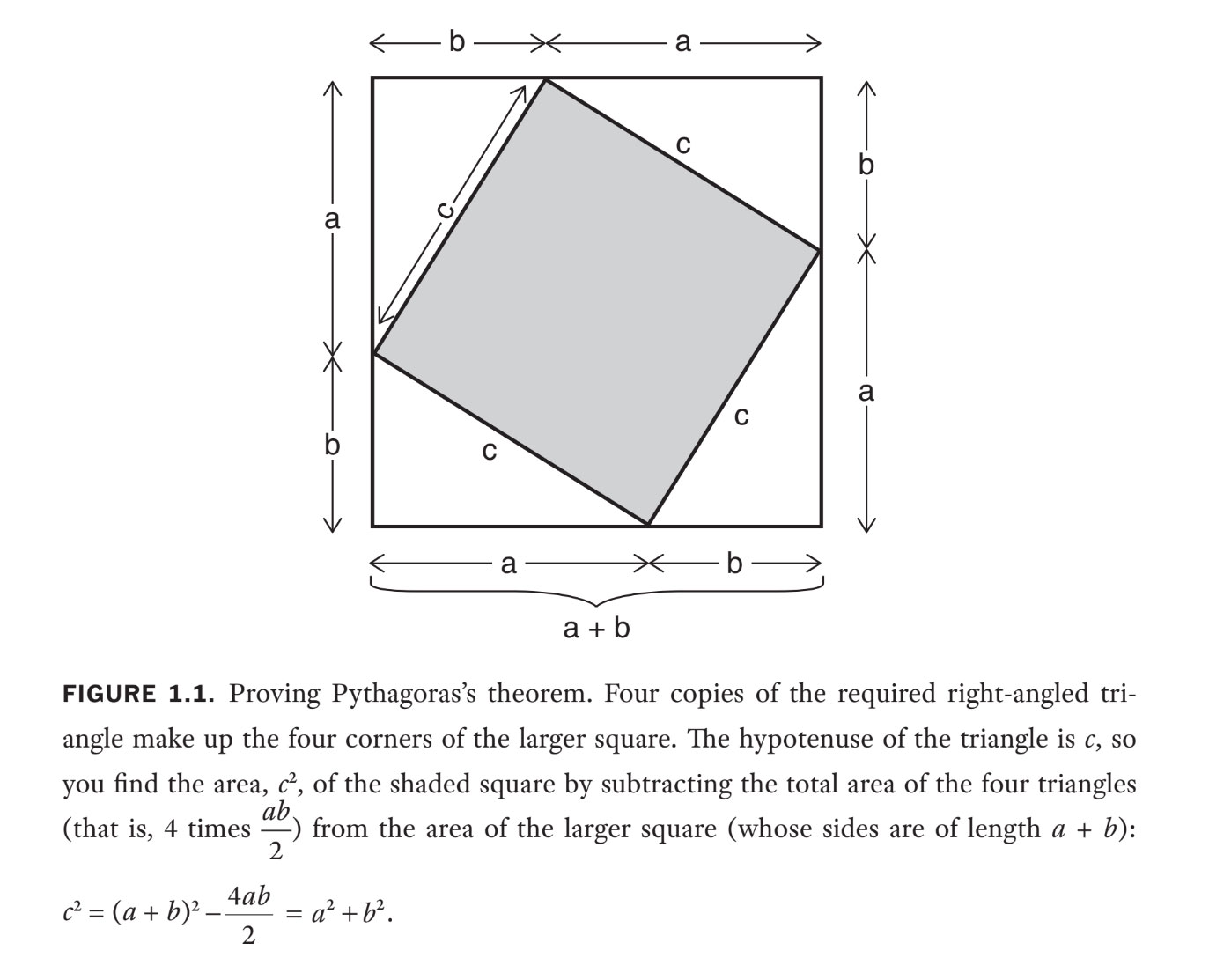
Deci „algebra” a fost comunicată în probleme de cuvinte greoaie sau diagrame din ce în ce mai complicate – deși geometria avea avantajele ei. De exemplu, este cel mai simplu mod de a demonstra teorema lui Pitagora. În figura 1.1, am oferit o adaptare algebrică a unei astfel de demonstrații, deși anticii pur și simplu au rearanjat diagrama pentru a arăta vizual că aria umbrită este egală cu suma ariilor pătratelor de pe laturile adiacente ale triunghiului – o abordare destul de inteligentă!

A fost nevoie de mult timp pentru ca algebra să iasă din aritmetică și geometrie ca un subiect separat. Nici măcar nu și-a primit numele până în epoca medievală și asta mulțumită matematicianului persan din secolul al IX-lea. Muhammed ibn-Mūsā (al-)Khwārizmī… A studiat la pionieratul universitate din Bagdad a lui Caliph al-Ma’mūn, sau „Casa Înțelepciunii”, când marea mișcare de traducere arabă era la apogeu: manuscrise grecești, indiene și alte manuscrise antice erau adunate din toate colțurile lumii. imperiu islamic în plină dezvoltare și tradus în arabă.

Imperialismul este rareori etic și adesea violent, dar poate duce în cele din urmă la fertilizarea culturală încrucișată și, în acest caz, mișcarea de traducere vizionară a fost atât de importantă încât, până în secolul al XII-lea, europenii învățau arabă pentru a traduce aceste manuscrise în latină – inclusiv al lui Ptolemeu”Almagestul” și “Elementele” ale lui Euclid, împreună cu noi lucrări arabe, cum ar fi cele ale lui al-Khwārizmī. Numele de “algebră” provine de la primul cuvânt din titlul cărții sale “Al-Jabr wa’l muqābalah” – care înseamnă ceva ca “Cartea Compendious despre calculul prin completare și echilibrare.”

Judecând după problemele incluse al-Khwārizmī, un exemplu de ceea ce a vrut să spună prin „Terminare” este „completând pătratul,” metoda pe care probabil ai fi învățat-o la școală pentru a rezolva ecuații patratice…

Nici Al-Khwārizmī nu a scris ecuații în forma simbolică pe care o folosim astăzi. De fapt, pentru ochii moderni, cartea sa este mai mult aritmetică decât algebrică, iar unul dintre impacturile sale importante în Europa, când a fost tradusă în latină, a fost popularizarea sistemului zecimal de numerație hindu-arabă, care a evoluat în cele din urmă în cel modern.

Cu toate acestea, Al-Khwārizmī este adesea numit „părintele algebrei”. S-ar putea să fi folosit mai degrabă cuvinte decât simboluri, iar problemele pe care le-a inclus s-ar putea să fi fost simple – scopul lui, ne spune el, a fost să-i învețe pe elevi cum să rezolve problemele de bază în „cazuri de moștenire, moșteniri, despărțiri, procese și comerț și în toate relațiile lor între ele sau în cazul în care măsurarea terenurilor, săparea canalelor, calculul geometric și alte obiecte de diferite feluri și feluri.”

Dar el a stabilit sistematic ecuații liniare și pătratice sub formă de cuvinte, cu metode algoritmice pentru rezolvarea lor – adică pentru găsirea „numerelor necunoscute”, a noastră modernă. Xlui și ylui. De fapt, cuvântul englezesc „algoritm” – adică un set de reguli pentru efectuarea unui calcul sau a unei alte operații – provine de la „algorismi”, o încercare timpurie latinizată de la Al-Khwārizmī.

…

Frumusețea ecuațiilor simbolice este că este mult mai ușor să vezi aceste modele generale atunci când poți vedea o problemă dintr-o privire. Comparați asta:

Take the square of the unknown number, then add the unknown number to itself and take the sum away from the square; now let the total be eight.

cu asta:

x^2–2x=8

Și mai sunt: ​​cei mai timpurii matematicieni au rezolvat fiecare ecuație separat, dar este mai ușor dacă poți vedea că orice metodă funcționează pentru ecuație x^2–2x=8 va funcționa și pentru orice ecuație de aceeași formă, x^2–ax=b. În cele din urmă, matematicienii antici au început să recunoască acest lucru, dar progresul a fost relativ lent, deoarece au trebuit să păstreze toate aceste tipare în cap, sau în propoziții lungi și complicate, și a fost ușor să-și piardă urma.

Primii care au publicat orice ecuație într-o formă simbolică transparentă, modernă, recunoscută au fost [Thomas] a lui Harriot executori în 1631, iar apoi [René] Descartes într-o apendice la „Discursul său despre metodă” din 1637. (Au existat câteva încercări anterioare, dar simbolismul – numit mai corect abreviere – a fost torturat și idiosincratic.) Chiar și semnele +, −, = și × pe care le luăm de la sine înțeles au intrat în uz pe scară largă abia în secolul al XVII-lea. Ceea ce înseamnă că algebriștii anteriori pe care îi cunoaștem – vechii mesopotamieni, egiptenii, chinezii și grecii, indienii medievali, perșii și arabii, precum și europenii moderni timpurii – toți și-au exprimat ecuațiile mai ales în cuvinte sau imagini picturale cu cuvinte. .

Legate de: 9 ecuații care au schimbat lumea

Este o abilitate singulară să gândești simbolic, așa cum arată această istorie lungă. Luați cuvântul problemă pe care l-am dat mai sus: este un exemplu de gândire algoritmică. Dar gândirea simbolică este algoritmică și nu numai, deoarece simbolurile sale conțin uneori semințele unui nou tip de creativitate – un nou tip de gândire de anvergură, dar economică.

Un caz clasic este Albert Einsteinlui E=mc^2. Einstein nu și-a propus să găsească legătura dintre energie și materie. Mai degrabă, el a vrut pur și simplu să calculeze energia cinetică a unui electron în mișcare conform noului său teoria relativitatiiastfel încât predicția lui teoretică să poată fi testată experimental.

Câteva luni mai târziu, însă, Einstein, în vârstă de 26 de ani, a început să-și dea seama de semnificația ecuației sale. El a scris-o în cea de-a cincea lucrare revoluționară din 1905, annus mirabilis, dar i-ar fi nevoie de încă doi ani pentru a dezvălui implicațiile complete și dramatice ale acestei relații simbolice. Pentru a realiza că acesta nu a fost doar un calcul despre o anumită formă de energie și un anumit tip de materie, a fost general: dacă un corp câștigă (sau pierde) energie, câștigă (sau pierde) și masă. Această idee bizară este străină de toată experiența noastră de bun simț – dar acolo era, ascunsă în simbolurile ecuației sale. Fizicienilor experimentali le-au luat zeci de ani pentru a confirma experimental această predicție matematică uimitoare.

Un exemplu mult mai simplu și mai vechi este succesiunea puterilor X, x^2, x^3 și așa mai departe. Prima „putere” este 1, deci X este într-adevăr x^1 , unde 1 a fost în mod tradițional legat geometric de o linie 1-D. Următoarele două, x^2 și x^3, se pronunță „x pătrat” și „x cub” prin analogie cu aria unui pătrat și volumul unui cub. Aceste nume evidențiază modul în care matematicienii timpurii au gândit mai degrabă geometric decât algebric, din cauza naturii tangibile a geometriei. În schimb, algebra simbolică este abstractă: trebuie să-i dai sens, chiar dacă este pur și simplu afișarea unui model interesant, cum ar fi x, x^2, x^3, x^4,… Dar această flexibilitate este marea putere a algebrei. Puteți nota câte puteri (finite) superioare doriți, fără a fi nevoie să le vizualizați ca obiecte fizice.

Acest lucru poate părea evident astăzi, dar a fost nevoie de trei mii și jumătate de ani pentru ca matematicienii să treacă de la rezolvarea ecuațiilor pătratice – „pătrat” derivă din latinescul „pătrat”, deci ecuațiile pătratice sunt cele a căror putere cea mai mare este x^2 (necunoscutul s-a înmulțit de la sine, așa cum spuneau anticii) — la rezolvarea ecuațiilor „cubice” și superioare. Aceste ecuații de grad superior sunt mult mai dificile, desigur; dar o parte din motivul pentru care soluțiile nu au venit ușor a fost că algebra a fost legată de cuvinte și imagini concrete pentru o perioadă atât de lungă.

De exemplu, am menționat „completarea pătratului” a lui Al-Khwārizmī pentru a rezolva o ecuație pătratică. Este de fapt o problemă veche de 4.000 de ani, care datează (din câte arată istoricul) de la tăblițele cuneiforme realizate de matematicieni care trăiesc, precum Al-Khwārizmī, în regiunea Irakului modern. Acești vechi mesopotamieni au rezolvat ecuații patratice completând literalmente un pătrat.

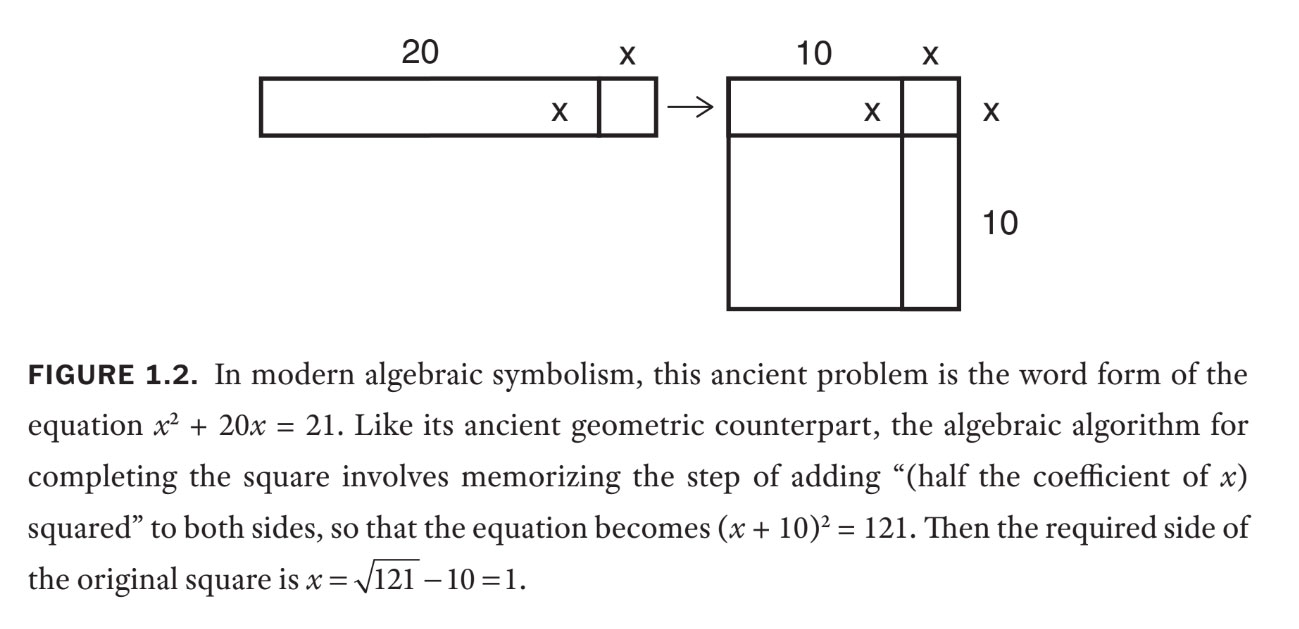
Aici este o problemă tipică de predare a vremii: „Adăugați 20 din lungimea mea la aria pătratului meu, [to get] 21. Cât de pătrat este pătratul meu?” Acest tip de problemă și algoritmul pentru rezolvarea acesteia sunt similare cu cele predate astăzi – cu excepția faptului că acum patru milenii, metoda a fost elaborată în întregime geometric. Mai întâi, desenați un pătrat cu latura arbitrară X (în notație modernă); apoi adăugați un dreptunghi cu dimensiunile 20 [by] X. Acum împărțiți acest dreptunghi suplimentar în două mai mici egale și aranjați-le lângă și sub pătratul original. În cele din urmă, completați acest pătrat nou, mai mare, ca în figura 1.2.

Mesopotamienii au avut probleme practice în minte când au dezvoltat această metodă, cel puțin inițial. Trăind într-un tărâm în care apa era la o primă, tăblițele lor conțin multe probleme legate de săpăturile de canale și rezervoare, capacitatea cisternelor, construcția și repararea barajelor și diguri și conturi administrative legate de aceste sarcini – și pentru a rezolva aceste probleme. , acești matematicieni antici au trebuit să rezolve ecuații referitoare la suprafețe și volume.

Aproape 3.000 de ani mai târziu, Al-Khwārizmī s-a concentrat și pe probleme practice similare și a folosit o metodă geometrică similară de completare a pătratului – la fel și alți matematicieni până în secolul al XVII-lea.

Robyn Arianrhod este un scriitor de știință și un matematician afiliat la Școala de Matematică a Universității Monash, unde cercetează relativitatea generală și istoria științei. Este autoarea cărților apreciate de critici „Eroii lui Einstein”, „Sedus by Logic” și „Thomas Harriot”.