
Timp de mii de ani, dacă doriți să trimiteți un mesaj secret, a existat practic o modalitate de a face acest lucru. Ați scăpa mesajul folosind o regulă specială, cunoscută doar pentru dvs. și publicului dvs. intenționat. Această regulă a acționat ca cheia unui blocaj. Dacă ai avea cheia, ai putea să scapi mesajul; În caz contrar, ar trebui să alegeți blocajul. Câteva încuietori sunt atât de eficiente, încât nu pot fi niciodată culese, chiar și cu timp și resurse infinite. Dar chiar și aceste scheme suferă de același călcâi al lui Ahile care plagiează toate aceste sisteme de criptare: Cum obțineți această cheie în mâinile potrivite, păstrând -o în același timp din cele greșite?
Soluția contraintuitivă, cunoscută sub numele de Cryptografia cheie publicănu se bazează pe păstrarea unui secret cheie, ci mai degrabă pe faptul că îl pune la dispoziție pe scară largă. Trucul este să folosești și o a doua cheie cu care nu -l împărtășești niciodată cu nimeni, chiar și cu persoana cu care comunici. Numai folosind această combinație de două chei – una publică, una privată – cineva poate scramble și a scăpa un mesaj.
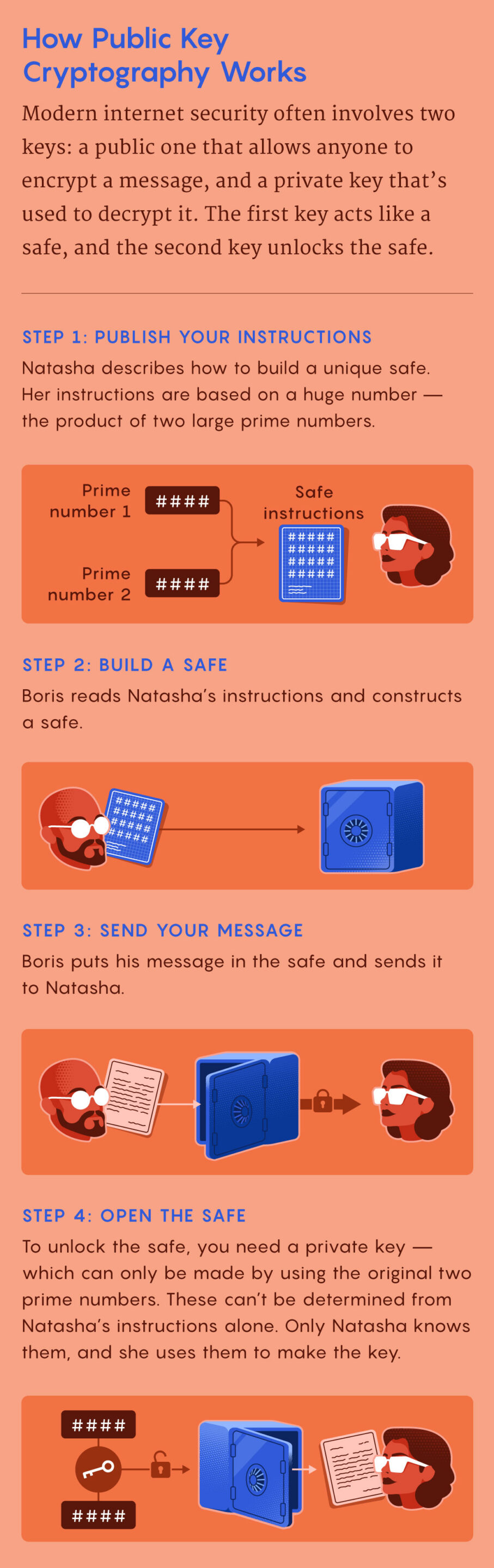
Pentru a înțelege cum funcționează acest lucru, este mai ușor să te gândești la „tastele” nu ca obiecte care se încadrează într -un blocaj, ci ca două ingrediente complementare într -o cerneală invizibilă. Primul ingredient face ca mesajele să dispară, iar al doilea îi face să reapară. Dacă un spion pe nume Boris dorește să -i trimită omologului său Natasha un mesaj secret, el scrie un mesaj și apoi folosește primul ingredient pentru a -l face invizibil pe pagină. (Acest lucru îi este ușor să facă: Natasha a publicat o formulă ușoară și cunoscută pentru dispariția cernelii.) Când Natasha primește hârtia pe poștă, ea aplică cel de-al doilea ingredient care face ca mesajul lui Boris să reapară.
În această schemă, oricine poate face mesaje invizibile, dar numai Natasha le poate face din nou vizibile. Și pentru că nu împărtășește niciodată formula pentru al doilea ingredient cu nimeni – nici măcar Boris – poate fi sigură că mesajul nu a fost descifrat pe parcurs. Când Boris dorește să primească mesaje secrete, el adoptă pur și simplu aceeași procedură: publică o rețetă ușoară pentru a face ca mesajele să dispară (pe care Natasha sau oricine altcineva îl poate folosi), păstrând în același timp unul doar pentru el însuși, ceea ce îi face să reapară.
În criptografia cu cheie publică, cheile „publice” și „private” funcționează la fel ca primul și al doilea ingrediente din această cerneală invizibilă specială: unul criptează mesaje, celălalt le decriptează. Dar în loc să folosească substanțe chimice, criptografia cheie publică folosește puzzle -uri matematice numite Funcții Trapdoor. Aceste funcții sunt ușor de calculat într -o direcție și extrem de dificil de inversat. Dar, de asemenea, conțin „capcane”, informații care, dacă sunt cunoscute, fac ca funcțiile să fie ușor de calculat în ambele direcții.
O funcție comună de capcană implică înmulțirea a două numere mari mari, o operație ușoară de efectuat. Dar inversarea acestuia – adică începând cu produsul și găsirea fiecărui factor principal – este practic din punct de vedere calcul. Pentru a face o cheie publică, începeți cu două numere mari mari. Acestea sunt capcanele tale. Înmulțiți cele două numere împreună, apoi efectuați câteva suplimentare Operații matematice. Această cheie publică poate acum cripta mesaje. Pentru a le decripta, veți avea nevoie de cheia privată corespunzătoare, care conține factorii primari – capcanele necesare. Cu aceste numere, este ușor să decriptați mesajul. Păstrați în secret acești doi factori primari, iar mesajul va rămâne secret.
Fundațiile pentru criptografia cheie publică au fost descoperite pentru prima dată între 1970 și 1974 de matematicienii britanici care lucrează pentru sediul guvernului din Marea Britanie, aceeași agenție guvernamentală care a crăpat codul enigma nazist în timpul celui de -al doilea război mondial. Munca lor (care a rămas clasificată până în 1997) a fost împărtășită cu Agenția de Securitate Națională a SUA, dar din cauza capacității de calcul limitate și costisitoare, niciun guvern nu a implementat sistemul. În 1976, cercetătorii americani Whitfield Diffie și Martin Hellman au descoperit primul cunoscut public Schema de criptografie cu cheie publicăinfluențat de criptograful Ralph Merkle. La doar un an mai târziu, algoritmul RSA, numit după inventatorii săi Ron Rivest, Adi Shamir și Leonard Adleman, au stabilit o modalitate practică de a utiliza criptografia cheie publică. Este încă în larg util, un bloc fundamental de construcție al internetului modern, care permite totul, de la cumpărături până la e-mail bazat pe web.
Acest sistem cu două chei face, de asemenea, posibile „semnături digitale”-dovadă matematică că un mesaj a fost generat de titularul unei chei private. Acest lucru funcționează deoarece cheile private pot fi folosite și pentru a cripta mesaje, nu doar pentru a le decripta. Desigur, acest lucru este inutil pentru păstrarea mesajelor secrete: dacă ați folosit cheia dvs. privată pentru a scramblea un mesaj, oricine ar putea folosi doar cheia publică corespunzătoare pentru a o dezgropa. Dar dovedește că tu, și numai tu, ai creat mesajul, deoarece deținătorul cheii private, numai tu ai fi putut cripta mesajul. Criptomonedele precum Bitcoin nu ar putea exista fără această idee.
Dacă două chei criptografice în loc de una sunt atât de eficiente, de ce a fost nevoie de milenii să descopere? Conform Russell Impagliazzoun informatician și teoretician al criptografiei la Universitatea din California, San Diego, conceptul de funcție de capcană nu a fost suficient de util înainte de invenția computerelor.
„Este o chestiune de tehnologie”, a spus el. “O persoană din secolul al XIX-lea s-a gândit la criptare ca fiind între agenții individuali cu informații militare în domeniu-literalmente, într-un câmp cu arme care trag. Deci, dacă primul tău pas este„ alegeți două numere primare de 100 de cifre pentru a se înmulți împreună, “bătălia se va termina înainte de a face asta.” Dacă reduceți problema la ceva ce un om poate face rapid, nu va fi teribil de sigur.
Povestea originală reimprimată cu permisiunea de la Revista Quantao publicație independentă editorială susținută de SimonsFoundation.
