
La 16 octombrie 1843, matematicianul irlandez William Rowan Hamilton a avut o epifanie în timpul unei plimbări pe lângă Canalul Regal din Dublin. Era atât de încântat încât și-a scos cuțitul și și-a sculptat descoperirea chiar atunci și acolo, pe Broome Bridge.
Este cel mai faimos graffiti din istoria matematicii, dar pare destul de modest:
i ² = j ² = k ² = ijk = –1
Cu toate acestea, revelația lui Hamilton a schimbat modul în care matematicienii reprezintă informațiile. Și acest lucru, la rândul său, a făcut nenumărate aplicații tehnice mai simple – de la calcularea forțelor la proiectarea unui pod, și RMN mașină sau o turbină eoliană, la programarea motoarelor de căutare și orientarea unui rover pe Marte. Deci, ce înseamnă acest faimos graffiti?
Obiecte rotative
Problema matematică pe care Hamilton încerca să o rezolve era cum să reprezinte relația dintre diferitele direcții în spațiul tridimensional. Direcția este importantă în descrierea forțelor și vitezelor, dar Hamilton a fost, de asemenea, interesat de rotațiile 3D.
Matematicienii știau deja să reprezinte poziția unui obiect cu coordonate precum x, y şi zdar a afla ce s-a întâmplat cu aceste coordonate atunci când ați rotit obiectul a necesitat o geometrie sferică complicată. Hamilton dorea o metodă mai simplă.
El a fost inspirat de un mod remarcabil de a reprezenta rotațiile bidimensionale. Trucul a fost să folosești ceea ce se numește „numere complexe“, care au o parte “reală” și un “imaginar” parte. Partea imaginară este un multiplu al numărului i„rădăcina pătrată a lui minus unu”, care este definită de ecuație i ² = –1.
Înrudit: Ar putea fi necesare numere imaginare pentru a descrie realitatea, arată noi studii
La începutul anilor 1800, câțiva matematicieni, printre care Jean Argand și John Warren, au descoperit că un număr complex poate fi reprezentat printr-un punct pe un plan. Warren a arătat, de asemenea, că este destul de simplu din punct de vedere matematic să rotiți o linie cu 90° în acest nou plan complex, cum ar fi întoarcerea unui ceas înapoi de la 12:15 până la 12 amiază. Căci asta se întâmplă când înmulți un număr cu i.
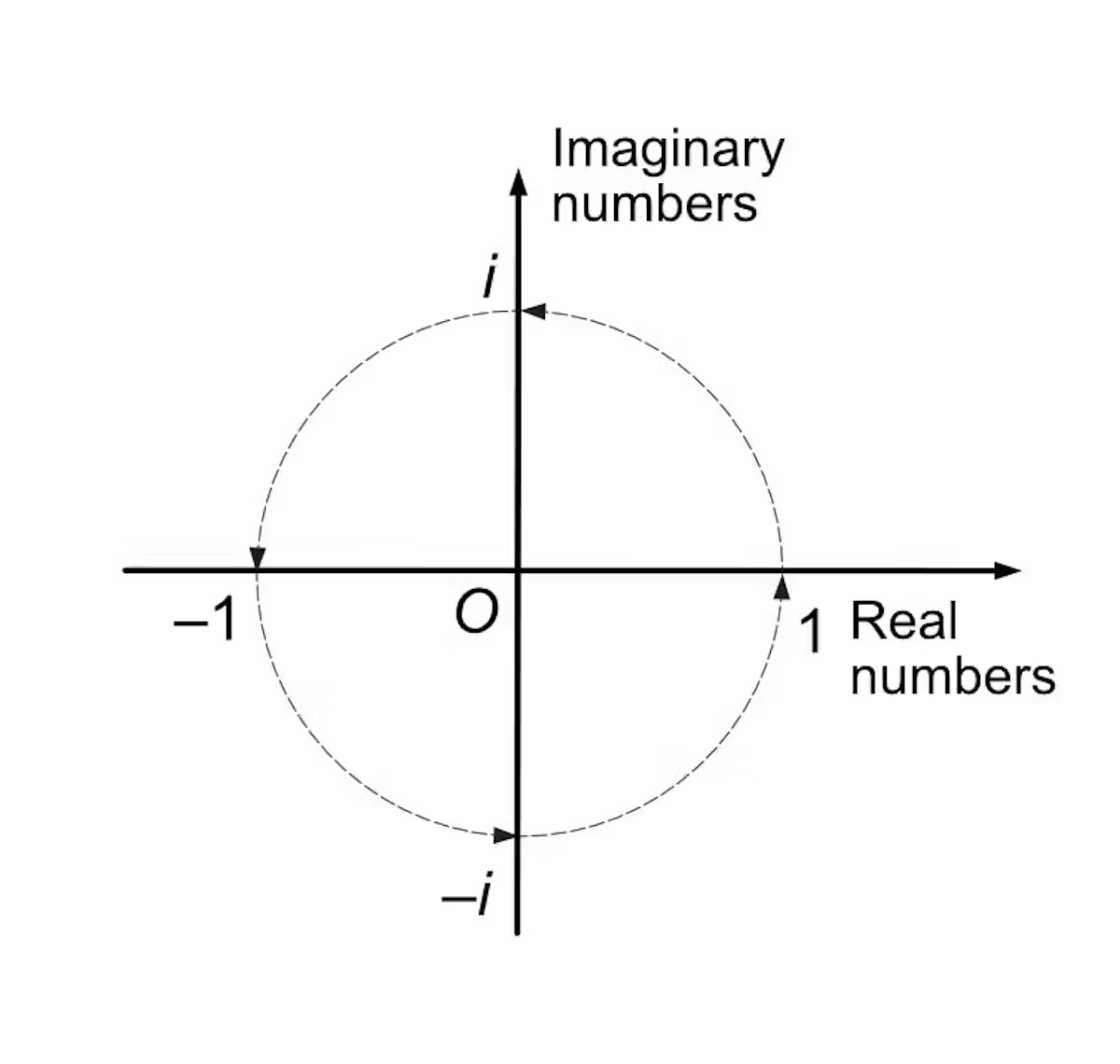
Hamilton a fost puternic impresionat de această legătură dintre numerele complexe și geometrie și a încercat să o facă în trei dimensiuni. El și-a imaginat un plan complex 3D, cu o a doua axă imaginară în direcția unui al doilea număr imaginar jperpendicular pe celelalte două axe.
I-au trebuit multe luni grele pentru a realiza că, dacă dorea să extindă vrăjitoria de rotație 2D a înmulțirii cu i avea nevoie patru-numere complexe dimensionale, cu a treilea număr imaginar, k.
În acest spațiu matematic 4D, k-axa ar fi perpendiculara pe celelalte trei. Nu numai că ar fi k fi definit de k ² = –1, este necesară și definiția sa k = ij = –ji. (Combinând aceste două ecuații pentru k dă ijk = –1.)
Punând toate acestea împreună, dă i ² = j ² = k ² = ijk = –1, revelația care l-a lovit pe Hamilton ca un fulger la Podul Broome.
Cuaternioni și vectori
Hamilton și-a numit numerele 4D „cuaternioni” și le-a folosit pentru a calcula rotațiile geometrice în spațiul 3D. Acesta este genul de rotație folosit astăzi pentru a muta un robot, să zicem, sau pentru a orienta un satelit.
Dar cea mai mare parte a magiei practice intervine atunci când iei în considerare doar partea imaginară a unui cuaternion. Căci acesta este ceea ce Hamilton a numit un „vector”.
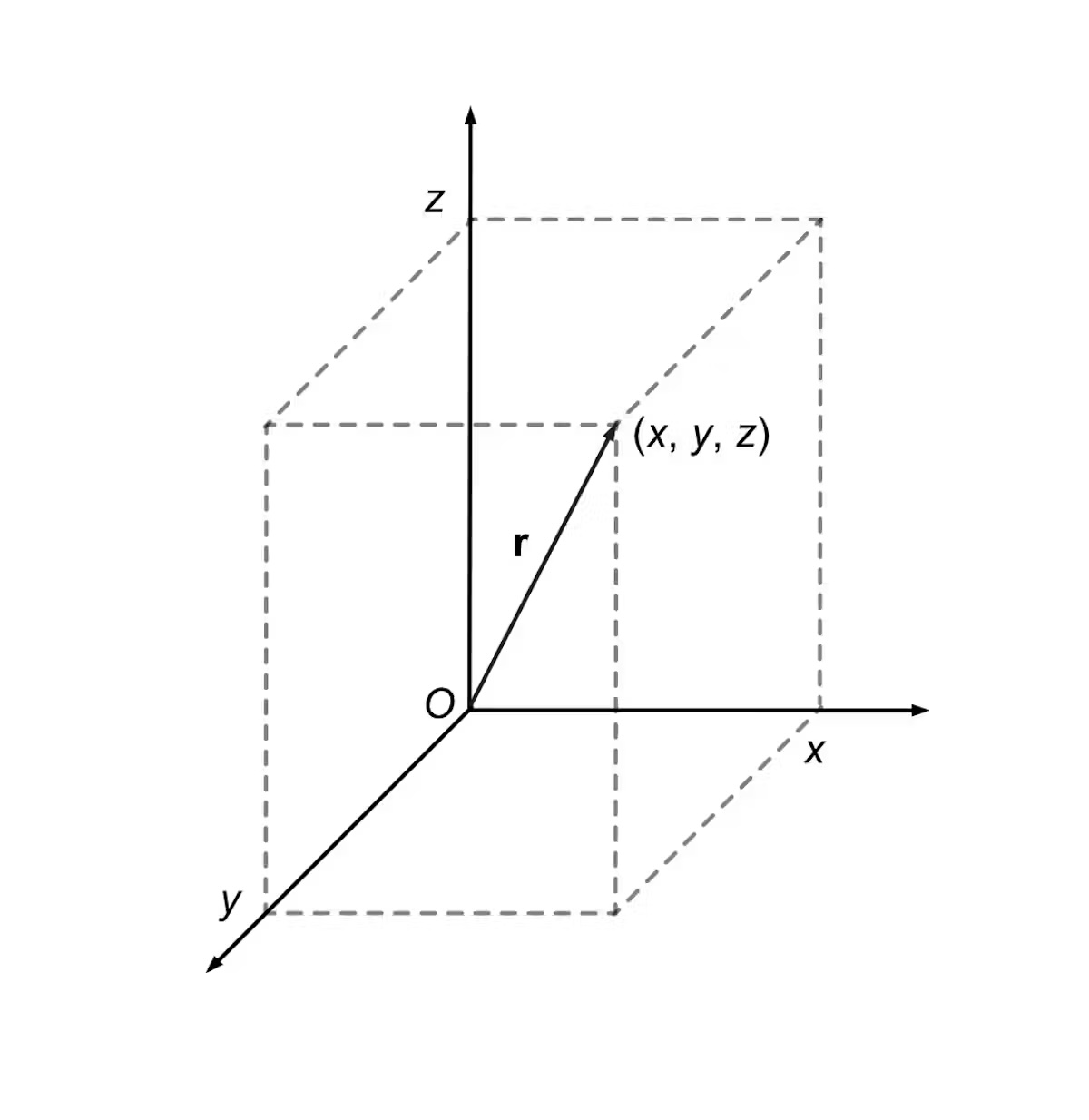
Un vector codifică două tipuri de informații în același timp, cel mai faimos amploarea și direcția unei mărimi spațiale, cum ar fi forța, viteza sau poziția relativă. De exemplu, pentru a reprezenta poziția unui obiect (x, y, z) relativ la „origine” (punctul zero al axelor de poziție), Hamilton a vizualizat o săgeată îndreptată de la origine la locația obiectului. Săgeata reprezintă „vectorul de poziție” x i + y j + z k.
„Componentele” acestui vector sunt numerele x, y şi z — distanța pe care săgeata se extinde de-a lungul fiecăreia dintre cele trei axe. (Alți vectori ar avea componente diferite, în funcție de mărimile și unitățile lor.)
O jumătate de secol mai târziu, excentricul telegraf englez Oliver Heaviside a contribuit la inaugurarea analizei vectoriale moderne, înlocuind cadrul imaginar al lui Hamilton. i, j, k cu vectori unitari reali, i, j, k. Dar, în orice caz, componentele vectorului rămân aceleași – și, prin urmare, săgeata și regulile de bază pentru multiplicarea vectorilor rămân și ele aceleași.
Hamilton a definit două moduri de a multiplica vectorii împreună. Unul produce un număr (acesta se numește astăzi produsul scalar sau punctual), iar celălalt produce un vector (cunoscut ca vector sau produs încrucișat). Aceste înmulțiri apar astăzi într-o multitudine de aplicații, cum ar fi formula pentru forța electromagnetică care stă la baza tuturor dispozitivelor noastre electronice.
Un singur obiect matematic
Fără să știe Hamilton, matematicianul francez Olinde Rodrigues a venit cu o versiune a acestor produse cu doar trei ani mai devreme, în propria sa lucrare despre rotații. Dar a numi înmulțirile lui Rodrigues produse de vectori este retrospectivă. Hamilton este cel care a legat componentele separate într-o singură cantitate, vectorul.
Toți ceilalți, de la Isaac Newton la Rodrigues, nu aveau nicio idee despre un singur obiect matematic care să unifice componentele unei poziții sau ale unei forțe. (De fapt, a existat o persoană care a avut o idee similară: un matematician german autodidact pe nume Hermann Grassmann, care a inventat independent un sistem vectorial mai puțin transparent în același timp cu Hamilton.)
Hamilton a dezvoltat, de asemenea, o notație compactă pentru a face ecuațiile sale concise și elegante. El a folosit o literă greacă pentru a desemna un cuaternion sau un vector, dar astăzi, după Heaviside, este obișnuit să se folosească o literă latină îngroșată.
Această notație compactă a schimbat modul în care matematicienii reprezintă mărimile fizice în spațiul 3D.
Luați, de exemplu, una dintre ecuațiile lui Maxwell care leagă câmpurile electrice și magnetice:
∇ × E = –∂B/∂t
Cu doar câteva simboluri (nu vom intra în semnificațiile fizice ale lui ∂/∂t și ∇ ×), aceasta arată cum un vector de câmp electric (E) se răspândește prin spațiu ca răspuns la schimbările din a câmp magnetic vector (B).
Fără notație vectorială, aceasta ar fi scrisă ca trei ecuații separate (una pentru fiecare componentă a B şi E) — fiecare câte o încurcătură de coordonate, înmulțiri și scăderi.
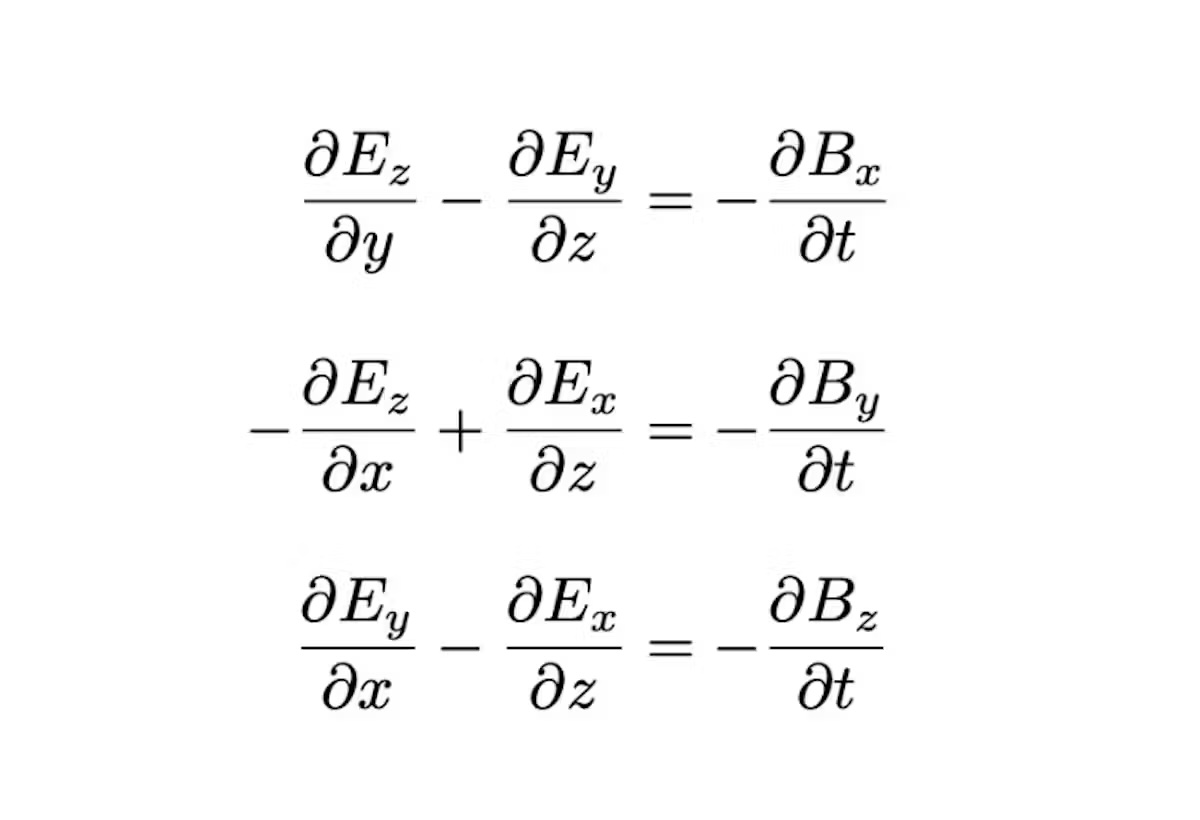
Puterea perseverenței
Am ales una dintre ecuațiile lui Maxwell ca exemplu, deoarece ciudatul scoțian James Clerk Maxwell a fost primul fizician important care a recunoscut puterea simbolismului vectorial compact. Din păcate, Hamilton nu a trăit să vadă susținerea lui Maxwell. Dar nu a renunțat niciodată la credința în noul său mod de a reprezenta cantitățile fizice.
Perseverența lui Hamilton în fața respingerii mainstream m-a emoționat cu adevărat, atunci când cercetam cartea mea despre vectori. Spera că într-o zi – „nu contează când” – i-ar putea fi mulțumit pentru descoperirea sa, dar asta nu era o vanitate. A fost entuziasm la posibilele aplicații pe care le-a avut în vedere.

Ar fi peste lună că vectorii sunt atât de folosiți astăzi și că pot reprezenta atât informații digitale, cât și fizice. Dar ar fi deosebit de mulțumit că, în programarea rotațiilor, cuaternionii sunt în continuare cea mai bună alegere – așa cum NASA iar programatorii de grafică pe computer știu.
În semn de recunoaștere a realizărilor lui Hamilton, pasionații de matematică reia faimoasa lui plimbare în fiecare 16 octombrie pentru a sărbători Ziua Hamilton. Dar cu toții folosim fructele tehnologice ale acelui graffiti modest în fiecare zi.
Acest articol editat este republicat din Conversația sub o licență Creative Commons. Citiți articol original.